Bonds play a significant role in the composition of most portfolios. so what are bonds?
Bonds are a type of financial instrument that represents a debt obligation. They are commonly used by governments, corporations, and other entities to raise capital.
When you purchase a bond, you are essentially lending money to the issuer in exchange for periodic interest payments and the return of the bond’s face value (the principal) at a specified future date, known as the maturity date.
Example:
Consider it this way: A bond operates much like a loan, representing a commitment to repay a debt.
To illustrate, think that you need $10,000, so you approach a bank. The bank assesses your creditworthiness to ensure you can repay the $10,000, and subsequently, they ask you to complete a contract.
Within this contract, there are several key elements. Firstly, it specifies the amount the bank is providing you, which is $10,000 in this instance. Secondly, it outlines the interest payments associated with the loan, which, in this case, amounts to 5% of the $10,000, equaling $500 per year. Lastly, the contract includes a maturity date, indicating that the bank is lending you this money for a period, such as 5 years. After you sign this document, it is referred to as an IOU (I Owe You).
| AMOUNT | $10000 |
| INTEREST RATE | 5% |
| COUPON PAYMENT | $500 |
| MATURITY PERIOD | 5 Years |
We can label this IOU as a bond. In essence, you are transferring ownership of this document to the bank. You present this piece of paper to the bank, which essentially states, “I will owe you $10,000, and I will make annual payments of $500 for 5 years, after which I will also repay the $10,000.” In exchange for this commitment, the bank provides you with the $10,000.
In reality, a bond essentially represents a debt obligation, effectively functioning as a loan. When you approach a bank, you might not perceive it in these terms; instead, you simply request and receive $10,000. Subsequently, you repay the interest over time, ultimately returning the initial sum at the end of the agreed-upon period. It’s essentially the same as if you were to sell a bond to your bank. If you possessed a bond, which is essentially an IOU stating, “I will owe you $10,000, and I will make annual payments of $500. After 5 years, I will repay the entire $10,000,” you can exchange it for the $10,000 from the bank. This is the fundamental mechanism behind how bonds function.
As mentioned earlier, governments issue bonds when they require capital to fund their operations. Similarly, corporations and companies opt for bond issuance when they need to raise funds through debt without diluting their ownership by attracting more shareholders. For instance, let’s consider Tesla (TSLA) as an example. Suppose Tesla needs funds to establish a new Gigafactory. In this scenario, they have two primary options:
- They can issue more shares and attract new shareholders, thereby increasing their capital base. However, this would also mean dividing profits among a larger number of shareholders.
- Alternatively, they can choose to obtain a loan by issuing bonds. This allows them to acquire the necessary capital without involving additional shareholders. The loan is then repaid, and any remaining funds can be distributed to the existing shareholders. This approach helps maintain a balance because having too many shareholders can lead to a dilution of ownership.
Companies typically strike a balance between equity (represented by shareholders’ investments) and debt (in the form of bonds) in their capital structure. Striking this balance is crucial because excessive debt can pose risks. If unforeseen financial difficulties arise, the bank or bondholders have a priority claim to the company’s assets and earnings, which they can use to recover their funds before shareholders receive any remaining proceeds.
IOUs, or bonds, play a pivotal role in financial markets as they serve as a fundamental mechanism for borrowing capital.
Terminologies of bonds
Issuer: The issuer is the entity that borrows money by issuing bonds. It can be a government (government bonds), a corporation (corporate bonds), a municipality (municipal bonds), or other organizations.
Face Value (Principal): The face value, also known as the par value or principal, is the amount of money that the bondholder will receive when the bond matures. It is typically a round number, such as $1,000 or $10,000.
Coupon Rate: The coupon rate is the fixed annual interest rate that the bond pays to the bondholder. It is expressed as a percentage of the bond’s face value. For example, a bond with a face value of $1,000 and a coupon rate of 5% will pay $50 in interest annually ($1,000 * 0.05).
Coupon Payment: This is the amount of interest paid to the bondholder at regular intervals, typically semiannually or annually. The coupon payment is calculated by multiplying the coupon rate by the face value of the bond.
Maturity Date: The maturity date is the date on which the bond will be redeemed, and the issuer will return the bond’s face value to the bondholder. Bonds can have short-term maturities (e.g., 1 year) or long-term maturities (e.g., 30 years or more).
Yield: The yield is the effective interest rate earned by the bondholder, taking into account the bond’s current market price. It can differ from the coupon rate if the bond is trading at a premium or discount to its face value. Yield can be expressed as current yield, yield to maturity (YTM), or yield to call (YTC) for callable bonds.
Credit Rating: Bonds are assigned credit ratings by credit rating agencies like Moody’s, Standard & Poor’s, and Fitch. These ratings indicate the creditworthiness of the issuer and the likelihood of the issuer defaulting on its debt obligations. Higher-rated bonds are considered less risky and typically offer lower yields.
Market Price: Bonds are bought and sold in the secondary market, and their prices can fluctuate based on various factors, including changes in interest rates, the issuer’s creditworthiness, and market demand. If a bond’s market price is higher than its face value, it is said to be trading at a premium; if it’s lower, it’s trading at a discount.
Callable and Noncallable Bonds: Some bonds are callable, meaning the issuer has the option to redeem the bonds before their maturity date. Callable bonds typically offer a higher coupon rate to compensate for this feature.
Convertible Bonds: Convertible bonds give bondholders the option to convert their bonds into a specified number of the issuer’s common shares. This feature can make convertible bonds attractive to investors seeking potential equity upside.
Zero-Coupon Bonds: These bonds do not pay periodic interest (coupon) payments. Instead, they are issued at a deep discount to their face value and provide a return when they mature.
Default Risk: All bonds carry some level of default risk, which is the risk that the issuer may not be able to make interest payments or repay the principal amount at maturity. Bonds with lower credit ratings have a higher default risk and typically offer higher yields to compensate for this risk.
Market price of a bond
In order to determine the price of a bond, it’s essential to grasp the concept of the present value of money, often abbreviated as PV.
Present value of money(PV):
The present value of money (PV), also known as discounted value or present discounted value, is a financial concept used to determine the current worth of a sum of money to be received or paid in the future. It’s based on the principle that the value of money diminishes over time due to factors such as inflation and the opportunity to earn interest on invested funds. Therefore, a dollar received today is generally worth more than a dollar received in the future.
Here are the key components and formula for calculating present value:
Future Value (FV): This is the amount of money you expect to receive or pay in the future. It’s important to know the future value you are trying to evaluate in terms of its present value.
Discount Rate (r): The discount rate represents the interest rate or rate of return that could be earned if the money were invested elsewhere. It’s used to discount future cash flows back to their present value. The choice of the discount rate can significantly affect the present value calculation.
Time Period (t): This is the number of periods between the present time (today) and the future time when the cash flow is expected. It can be expressed in years, months, or any other relevant time unit.
The formula for calculating the present value (PV) of a future sum of money is:
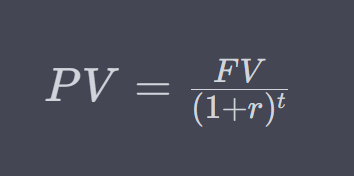
In this formula:
- PV = Present Value
- FV = Future Value
- r = Discount Rate
- t = Time Period
Here’s how the formula works:
- Divide 1 by (1+r), which accounts for the time value of money (discounting).
- Raise the result to the power of t, which represents the number of time periods.
- Finally, divide the future value (FV) by the result from step 2 to find the present value (PV).
Example:
For instance, let’s say I approached you and asked if you could loan me $100, with the promise to repay exactly $100 in one year. What would your response be? You’d probably hesitate because $100 today doesn’t hold the same value as $100 a year from now. If you had the option to invest that $100 or deposit it in a bank offering a 5% interest rate, you’d have $105 at the end of the year, right? So, if you were to lend me $100, it would be reasonable to charge me interest—specifically, 5%. Therefore, I should repay you $105, as that’s the amount you could have earned by having the money in a bank.
Conversely, if I were to say, “I’ll repay you $100 in a year,” how much would you be willing to give me right now? To determine the present value of $100 one year from now, we can use the present value formula with the current interest rate at 5%. This involves dividing $100 by 1.05, which yields $95.24. What this signifies is that $100 to be received in a year is equivalent to $95.24 in today’s terms. Why? Because if you take $95.24 and apply a 5% interest rate to it(95.24*1.05), it will grow to $100.
This is the method for calculating bond prices. Let’s say you have a bond with a 5-year maturity, with a face value of $10,000. At the end of 5 years, you need to repay the full $10,000. Additionally, you have to pay 5% interest each year. yields 5%. So, how much is the bond worth today?
To calculate the present value of the bond:
- The $500 interest payment from the first year, discounted at a 5% interest rate, is equivalent to $476.19 today.
- For the second year’s $500 interest, which is two years away, the present value is $453.51.
- In the third year, the $500 interest is three years away and has a present value of $431.92.
- In the fourth year, the present value of the $500 interest, four years away, is $411.35.
- Lastly, for the final payment of $10,000 plus the $500 interest in the fifth year, which is five years away, the present value is $8,227.02.
Adding up all these present values gives a total of $476.19 + $453.51 + $431.92 + $411.35 + $8,227.02, which sums up to $10,000.
You might wonder why we go through all this when the bond’s face value is $10,000, and its current market value is also $10,000. The key lies in understanding the impact of interest rates. In our example, the bond has a face value of $10,000, a maturity period of 5 years, a coupon rate of 5%, and its current market price matches the face value, which is $10,000. The bond yield, the return you’d get from owning this bond, is also 5%. If you own this bond, you’re essentially earning a 5% annual return because you’re lending money to someone who is paying you 5% per year and returning your full amount at the end of the period.
Now, let’s consider what happens when the interest rate rises. Suppose the interest rate is now 6%. In that case, a new bond with the same terms but offering a 6% return becomes available. People may hesitate to buy the 5% bond because the new bond offers a better return. To make the old 5% bond more attractive, its price needs to decrease, so investors can achieve a return closer to the 6% market rate.
So, if we recalculate the present values of the bond’s coupon payments and face value, using a 6% discount rate (the current market rate), the values change. The present values are as follows:
- First year: $471.70
- Second year: $445.00
- Third year: $419.81
- Fourth year: $396.04
- Fifth year (with face value): $7,846.21
If we add all these values together: $471.70 + $445.00 + $419.81 + $396.04 + $7,846.21, the total is $9,578.82.
Now, because the market interest rates are higher, people are not willing to pay the full $10,000 for the bond. They would consider buying the old 5% bond only if they could purchase it at a lower price. This way, they would earn a 6% return by investing less than $10,000. By investing $9,578.82 and receiving $500 each year, plus the $10,000 at the end, they would achieve the current market rate of return.
The bond price is subject to change depending on prevailing interest rates. If you own a bond that pays a high interest rate and market interest rates rise, the value of your bond will decrease. Conversely, if you have a bond with a high interest rate, and market interest rates decline, the price of your bond will increase. This happens because investors are attracted to bonds that offer higher interest rates, and they are willing to pay more for them. They bid up the bond’s price to the extent that, if they purchase it, they can achieve a return equivalent to the lower current market interest rate. As the bond owner, this situation allows you to sell the bond at a profit.
Conclusion
In conclusion, bonds are essential financial instruments that play a vital role in both the global economy and the financial markets. They serve as a means for governments, corporations, and other entities to raise capital, and they offer investors a relatively stable and predictable income stream. The key characteristics of bonds include their face value, coupon rate, maturity date, and market price. Understanding the concepts of yield, price fluctuations, and the relationship between interest rates and bond prices is crucial for investors.
Bonds come in various types, including government bonds, corporate bonds, municipal bonds, and more, each with its own risk and return profile. The choice of which bond to invest in depends on an individual’s financial goals, risk tolerance, and time horizon.